Roteiro preparado para aula sobre diagnóstico de modelos da disciplina BIE5781 Modelagem Estatística para Ecologia e Recursos Naturais do Programa de Pós-Graduação em Ecologia da Universidade de São Paulo.
Comentários e questões, por favor fale com Melina.
Para mais detalhes, veja a vinheta do pacote.
OBS: Este roteiro também está disponivel no site do Rpubs.
Primeiro, carregando os pacotes que serão usados:
library(DHARMa)
library(lme4)
library(glmmTMB)
library(ggplot2)Visão geral das funções do DHARMa
Vamos primeiro gerar 200 observações de uma distribuição Poisson com uma variável ambiental com a função createData do próprio pacote DHARMa:
set.seed(1234) # para garantir que todos tenhamos os mesmos resultados
testData = createData(sampleSize = 200, intercept = 0, fixedEffects = 1,
numGroups = 10, randomEffectVariance = 1,
family = poisson())Olhando a cara dos dados:
head(testData) ## ID observedResponse Environment1 group time x y
## 1 1 0 0.68330509 1 28 0.5063586 0.9770535
## 2 2 0 -0.16955524 1 80 0.8212286 0.5117742
## 3 3 1 0.78339199 1 150 0.5447566 0.4671612
## 4 4 2 -0.58651859 1 101 0.2666845 0.7238355
## 5 5 2 0.90039742 1 111 0.3446373 0.1420736
## 6 6 0 -0.04308309 1 137 0.3691760 0.5235778observedResponseé a variável resposta, vindo de uma Poisson variando entre 0 e 13.
Environment1é a variável preditora ambiental.
groupé a variável de agrupamento, digamos locais amostrados, regiões, blocos de experimentos, etc.
timeseria uma variável que indica tempo, mas não estamos usando neste exemplo. Logo esse tempo é aleatóriamente definido nos dados (valores de 1 a 200).
xeyseriam as coordenadas espaciais das observações, mas também não estamos usando nesse exemplo. Logo os valores são tirados de uma distribuição uniforme entre 0 e 1).
ggplot(testData, aes(y = observedResponse, x = Environment1, col = group))+
geom_point() +
theme_classic()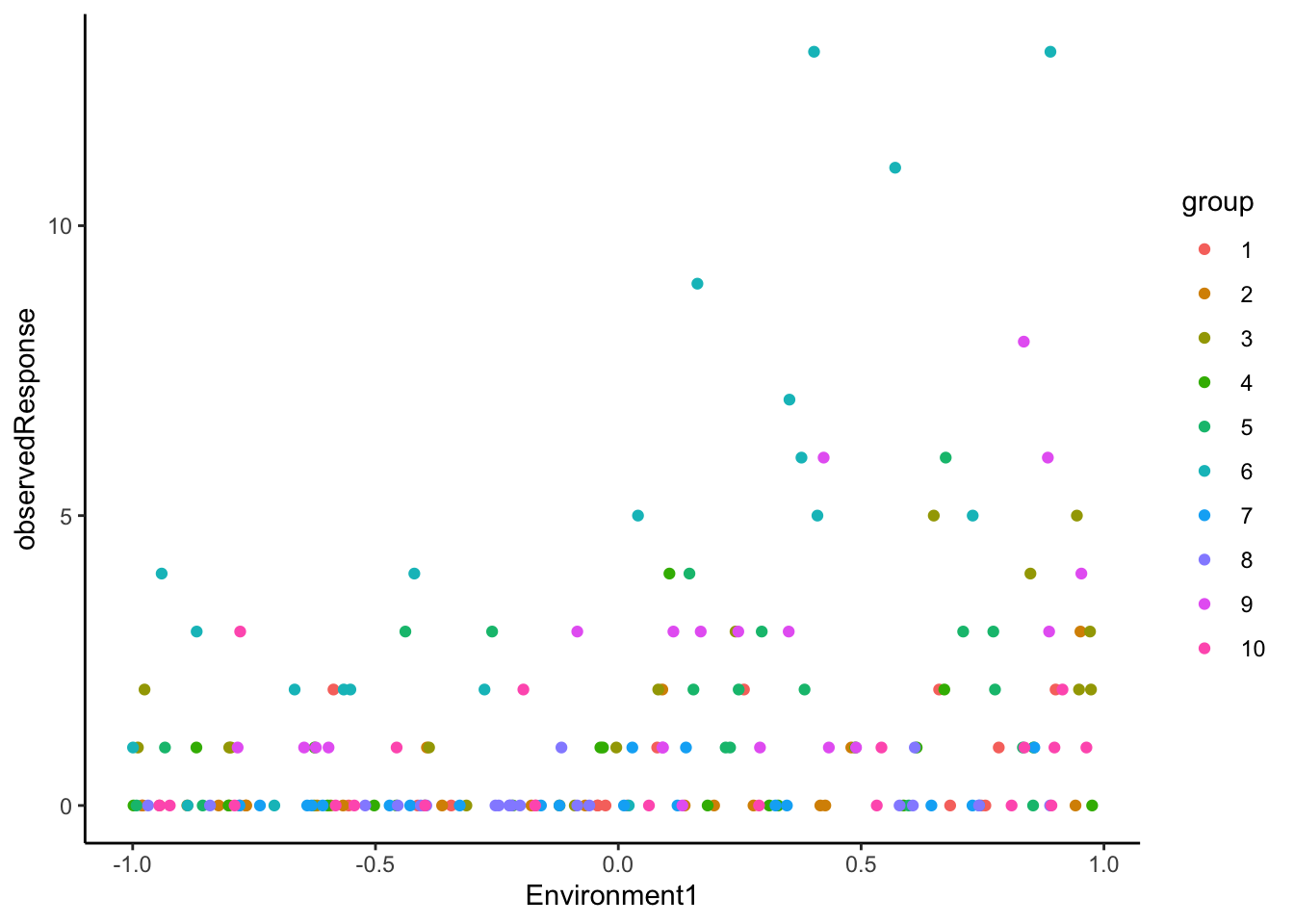
Agora vamos ajustar o modelo correto para este dados, usando um GLMM Poisson da variável resposta em função da variável preditora ambiental e o intercepto aleatório de grupo, com o pacote lme4:
fittedModel <- glmer(observedResponse ~ Environment1 + (1|group),
family = "poisson",
data = testData)Calculando os resíduos padronizados
Usamos a função simulateResiduals, que por padrão vai gerar 250 simulações1, para calcular os resíduos quantílicos para cada observação:
res <- simulateResiduals(fittedModel)Os principais gráficos de resíduos do DHARMa
plot(res)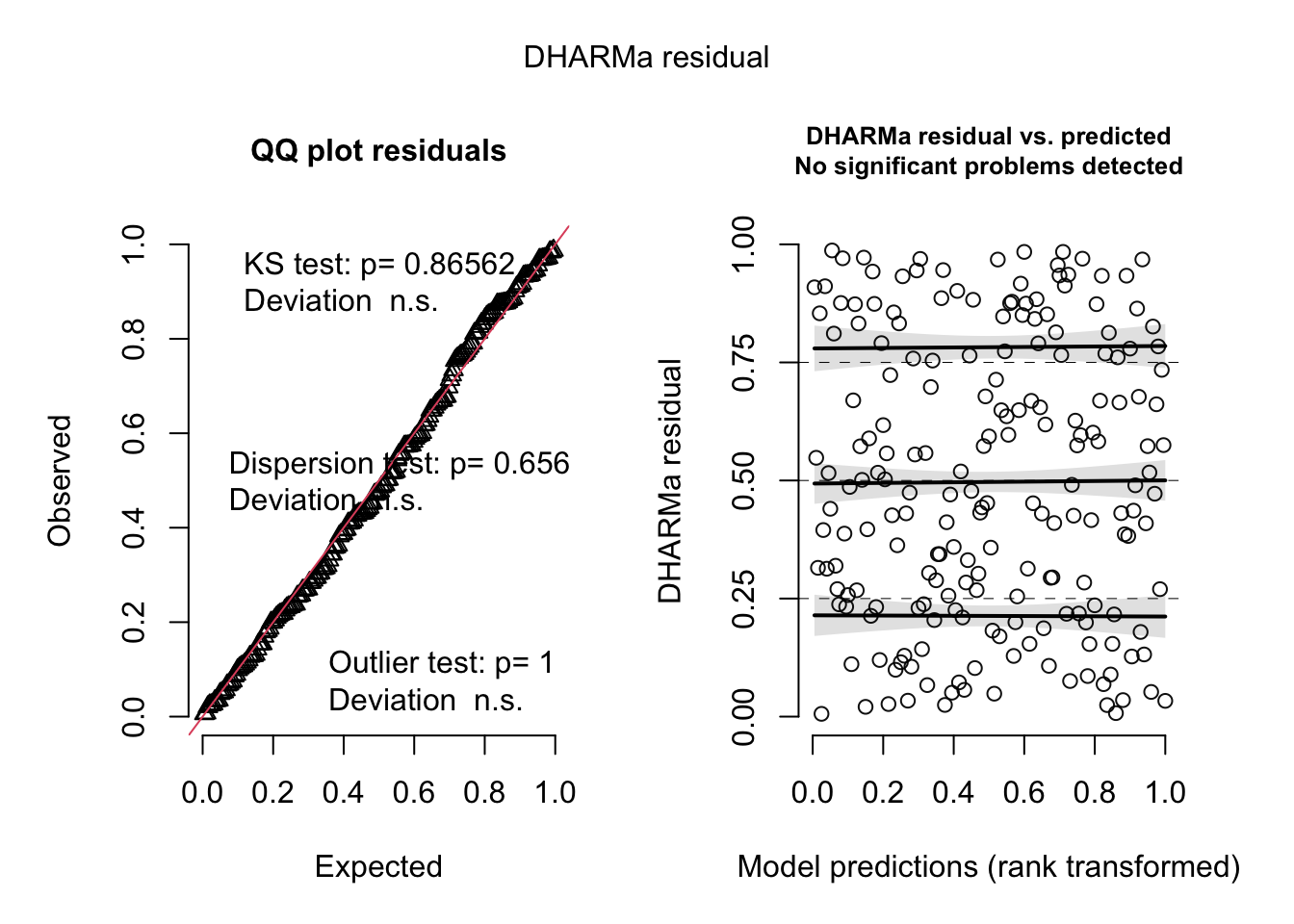
Interpretação do painel esquerdo:
- Gráfico quantil-quantil dos resíduos (Observed) e de uma distribuição uniforme (Expected).
- Teste de uniformidade KS (Kolmogorov-Smirnov). Essencialmente, a mesma informação que o QQ, mas em forma de teste e com p-valor para os que gostam.
- Teste de dispersão (padrão): compara a variância das observações com a variância das simulações.
- Testes de valores extremos/outliers: testa se o número de outliers (ou seja, observações fora do envelope da simulação) é maior/menor do que seria esperado sob H0 (modelo corretamente especificado).
Interpretação do painel direito:
- DHARMa resíduos ~ preditos. Esperamos uma distribuição completamente uniforme na direção y. Para isso, são feitas linhas de tendência com GAMs (generalized additive models) dos quantis ajustados nos resíduos em 0,25, 0,5, 0,75. Se for detectada alguma tendência, as linhas serão destacados em vermelho.
Esses gráfico também podem ser criados separadamente com as seguintes funções :
# testes podem ser omitidos, se preferir
plotQQunif(res,testUniformity = F,testOutliers = F,testDispersion = F) 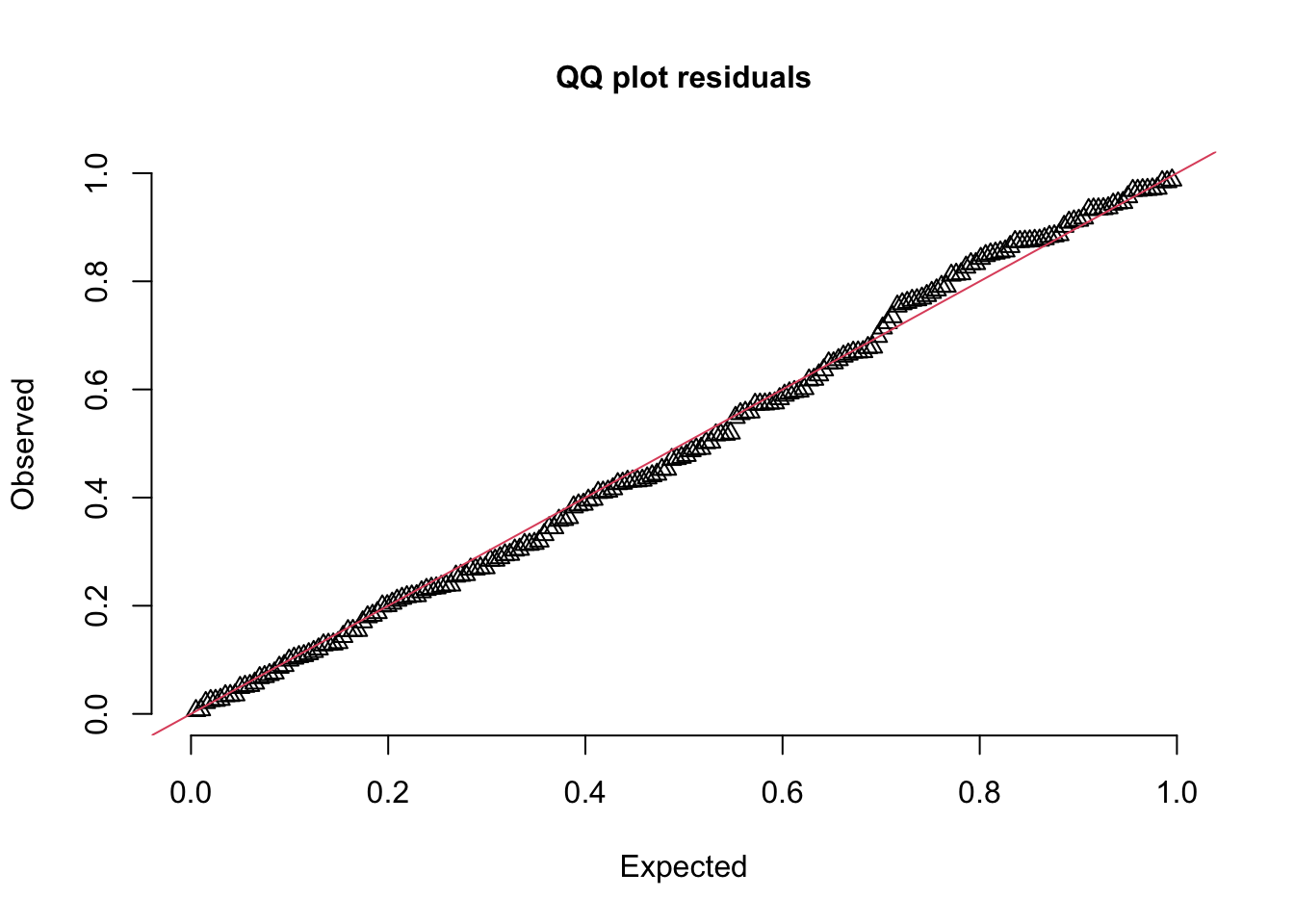
# predições são geralmente tranformadas em ranking para facilitar observação,
# principalmente para distribuições cujas predições são distorcidas (skewed)
# mas podemos desligar se quisermos:
plotResiduals(res, rank=F)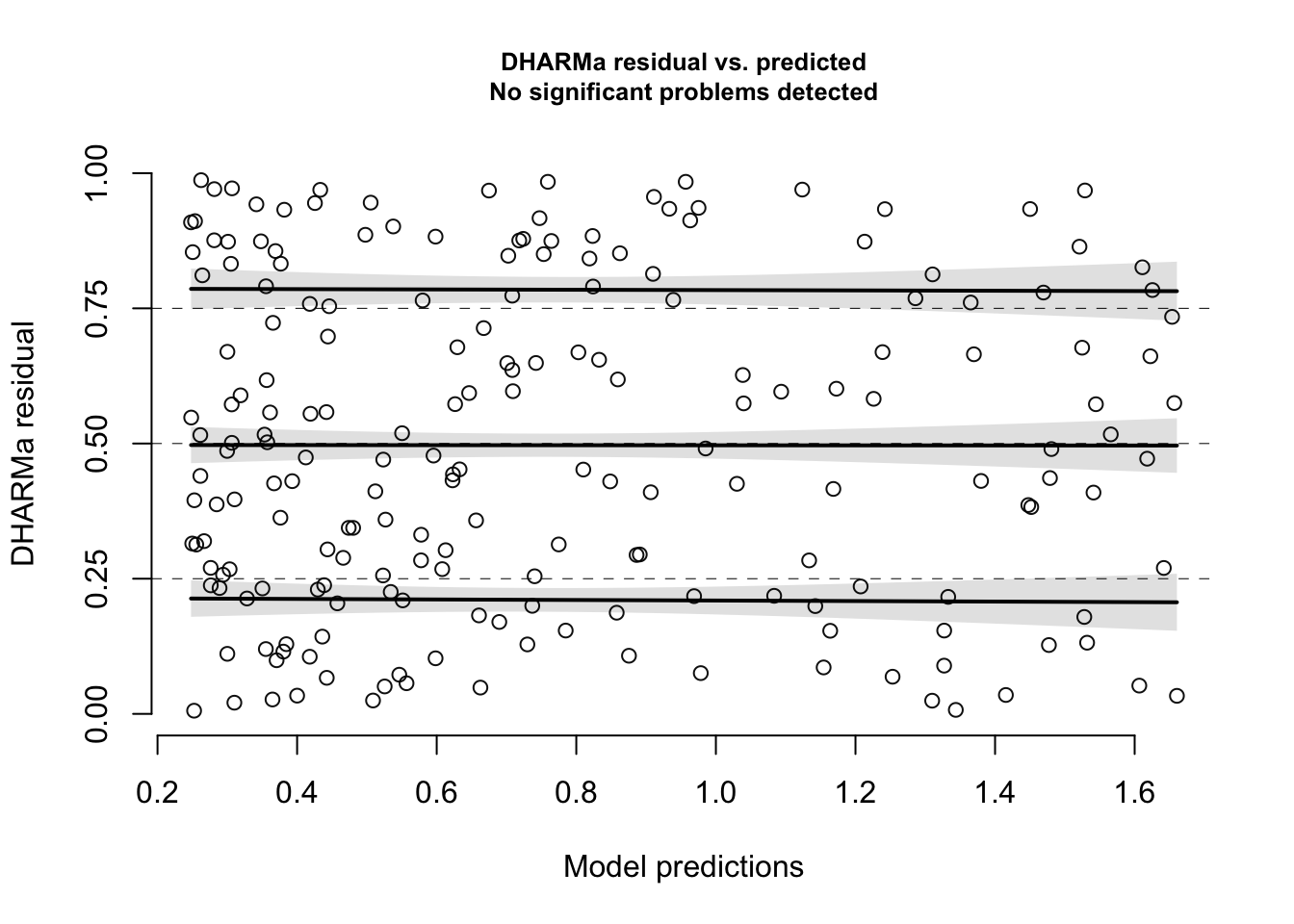
Testes disponíveis
Os testes acima também pode ser realizados separadamente e com mais profundidade (e gráficos adicionais) a partir das funções de cada teste. Lembrando que, segundo nossa hipótese H0 de que o modelo está corretamente especificado, esperamos que os valores de p não sejam significativos.
Uniformidade
Avaliando se os resíduos se conformam como uma distribuição normal. Teste de Kolmogorov-Smirnov (KS).
testUniformity(res, plot=F) # o plot é o meso do plotQQunif, vc pode desligá-lo##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: simulationOutput$scaledResiduals
## D = 0.042355, p-value = 0.8656
## alternative hypothesis: two-sidedSobre ou subdispersão
Sobre/subdispersão significa que os dados observados são mais/menos dispersos do que o esperado de acordo com o modelo ajustado.
Nesse teste, avaliando se a variância dos resíduos é consistente com a variância esperada. Essa função oferece diferentes testes a partir dos argumentos escolhidos, veja o help ?testDispersion para mais detalhes. O histograma apresentado pelo teste é o da distribuição das variâncias dos resíduos simulados e a variância dos resíduos observados (linha horizontal vermelha).
A estatística D é a razão entre o observado e esperado, com valores acima de 1 indicando sobredispersão e abaixo de 1 indicando subdispersão.
testDispersion(res)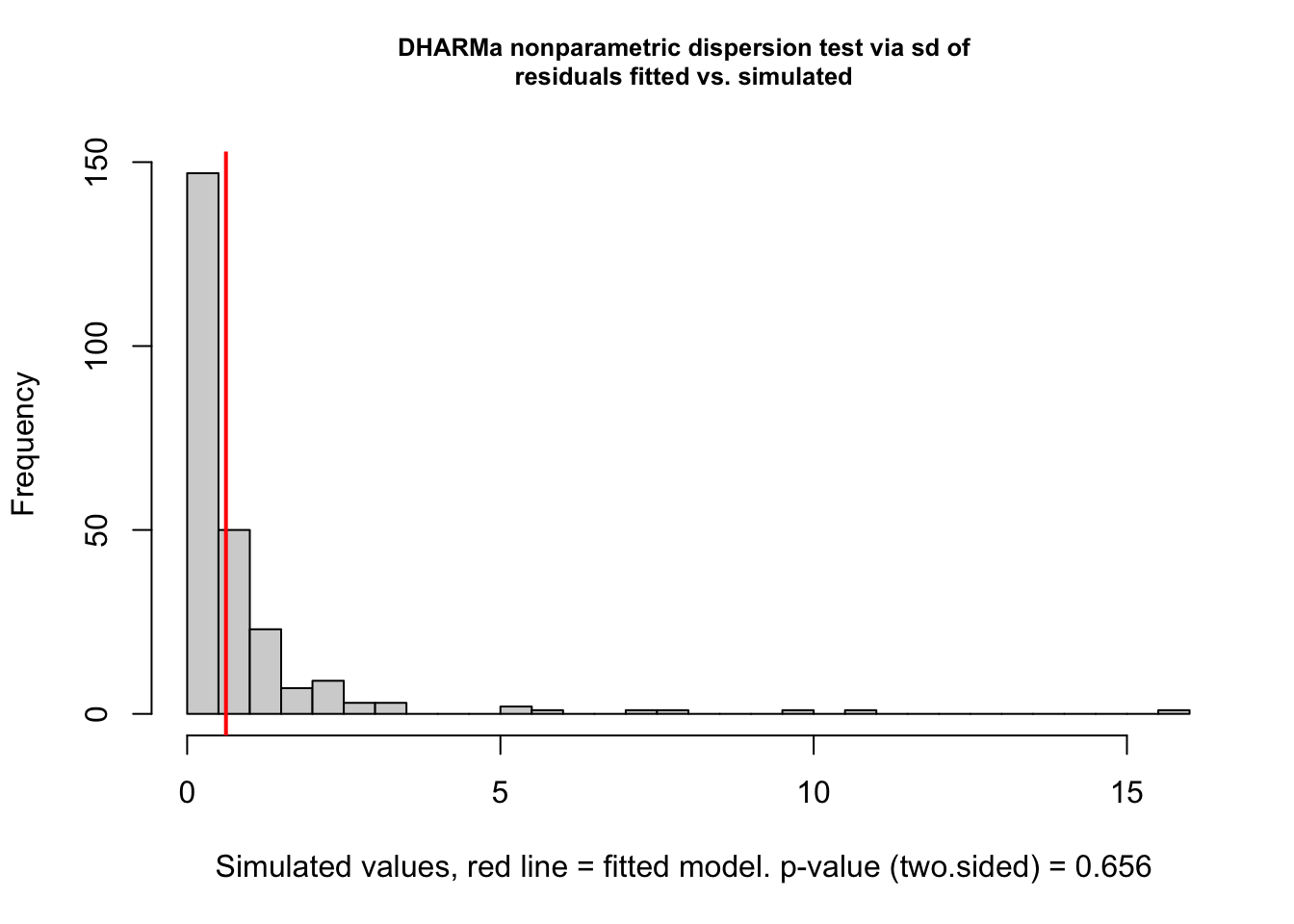
##
## DHARMa nonparametric dispersion test via sd of residuals fitted vs.
## simulated
##
## data: simulationOutput
## dispersion = 0.70258, p-value = 0.656
## alternative hypothesis: two.sidedValores extremos / outliers
Testa se o número de outliers (observações fora do envelope de simulação) é maior/menor do que seria esperado sob H0 (modelo corretamente especificado).
Importante ressaltar que a interpretação destes outliers não é a mesma para outliers em modelos lineares gaussianos.
Aqui estamos comparando se o valor observado é maior ou menor do que todos os valores simulados para aquela observação. Pode acontecer que todos os valores simulados para aquela observação são maiores do que o valor observado, recebendo então o resíduo desta observação o valor 0. Se todos os valores simulados são menores do que o valor observado, o resíduo desta observação recebe o valor 1. Logo, o teste depende do número de simulações que você estipulou na função simulateResiduals(); quanto mais simulações, menor a chance de outliers.
O gráfico mostra a distribuição dos resíduos e se houver outliers, eles serão destacados nos cantos 0 e 1 do eixo x.
testOutliers(res)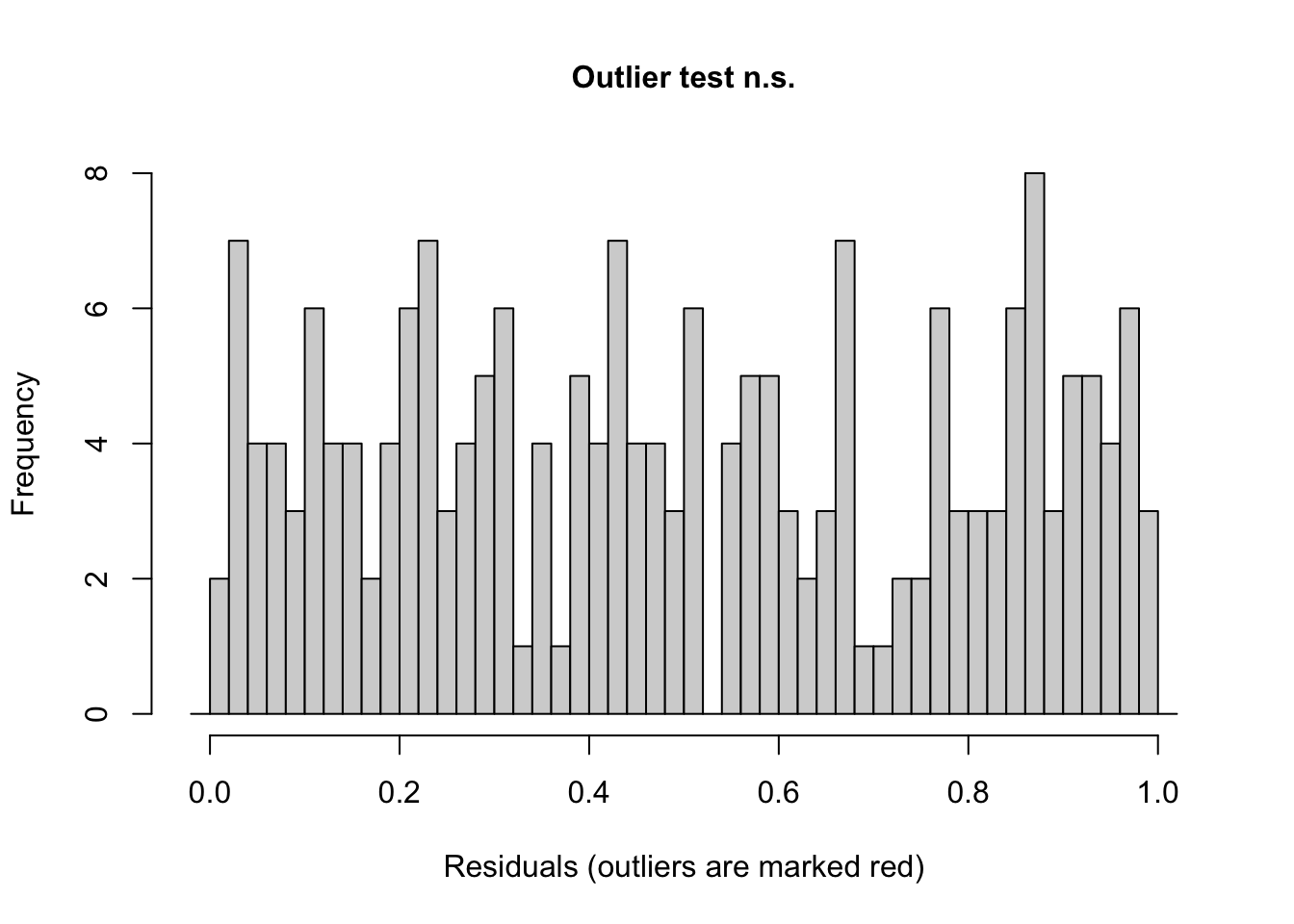
##
## DHARMa bootstrapped outlier test
##
## data: res
## outliers at both margin(s) = 0, observations = 200, p-value = 1
## alternative hypothesis: two.sided
## percent confidence interval:
## 0.000000 0.037625
## sample estimates:
## outlier frequency (expected: 0.00515 )
## 0Teste quantis Resíduo ~ predito
Testa se existe alguma relação não esperada entre os resíduos e as predições. Para avaliar essa ausência de relação, são ajustadas 3 GAMs (generalized additive models) nos quantis 0,25, 0,5, 0,75. Se esses GAMs se desviarem significativamente de uma linha reta nesses valores, eles serão destacados (em vermelho). O valor de p do teste abaixo, sem o plot, é uma combinação dos 3 valores de p com correção para múltiplos testes.
testQuantiles(res, plot=F)##
## Test for location of quantiles via qgam
##
## data: res
## p-value = 0.4347
## alternative hypothesis: bothDados zero-inflado
Verificar se há mais zeros nos dados do que o esperado pela distribuição. O histograma mostra a quantidade de zeros vindo das simulações e a quantidade de zeros observada (linha vermelha vertical). O teste de zero-inflação é um teste de diferença entre a quantidade de zeros observada e a quantidade de zeros esperada.
testZeroInflation(res)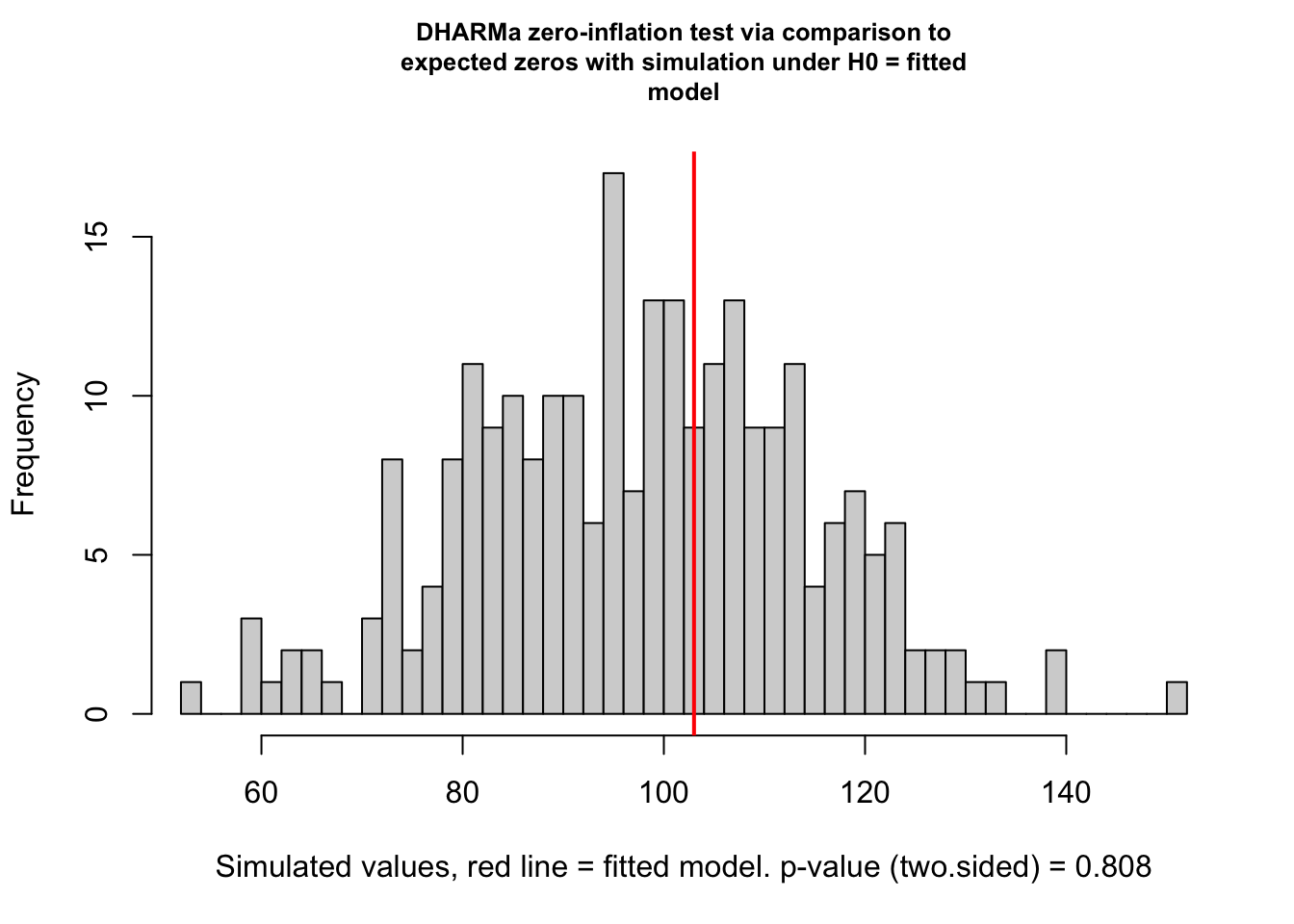
##
## DHARMa zero-inflation test via comparison to expected zeros with
## simulation under H0 = fitted model
##
## data: simulationOutput
## ratioObsSim = 1.0491, p-value = 0.808
## alternative hypothesis: two.sidedAutocorrelação espacial
Detecta se há indícios de autocorrelação espacial nos resíduos. Para isso, precisa prover os valores das coordenadas dos dados. Aqui estamos usando as variáveis x e y do nosso conjunto de dados, mas elas são aleatoriamente geradas e não representam uma estrutura espacial real.
testSpatialAutocorrelation(res, x = testData$x, y = testData$y )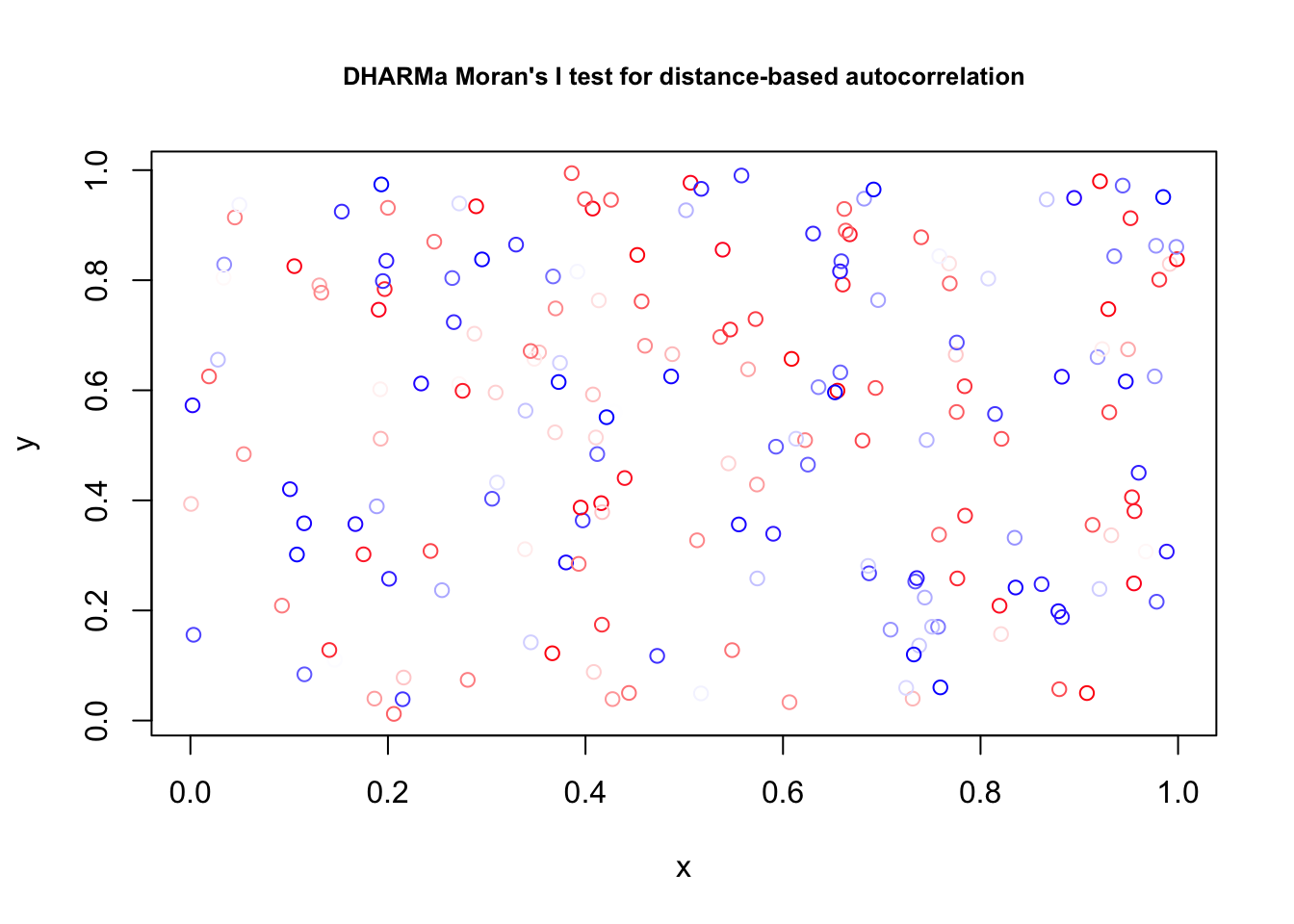
##
## DHARMa Moran's I test for distance-based autocorrelation
##
## data: res
## observed = -0.0071370, expected = -0.0050251, sd = 0.0099197, p-value =
## 0.8314
## alternative hypothesis: Distance-based autocorrelationTeste de autocorrelação temporal
O mesmo para autocorrelação temporal, mas aqui precisamos de uma variável temporal (sequencia de acontecimentos). Vamos usar a variável time do nosso conjunto de dados, mas ela é aleatoriamente gerada e não representa uma estrutura temporal real.
testTemporalAutocorrelation(res, time = testData$time)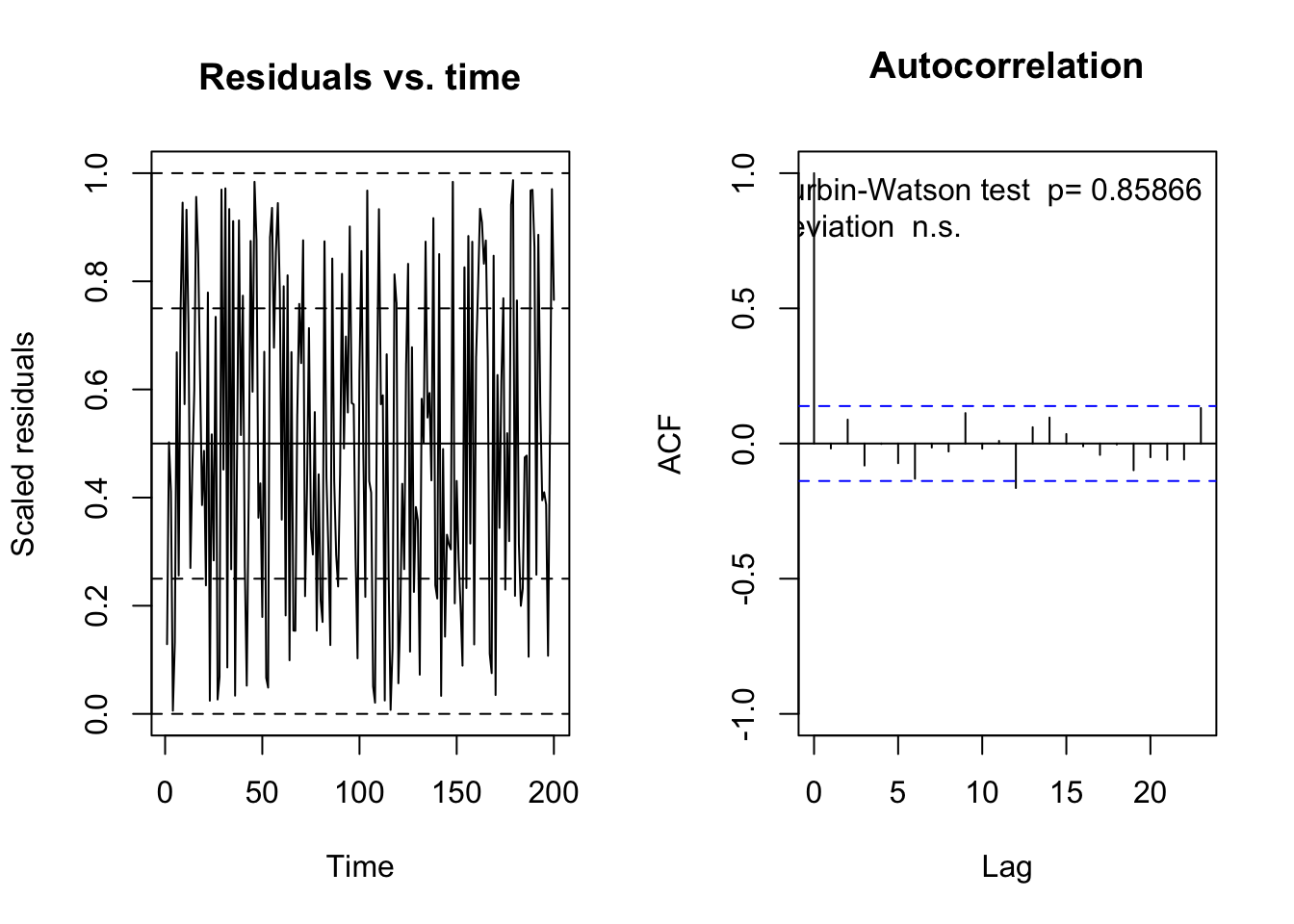
##
## Durbin-Watson test
##
## data: simulationOutput$scaledResiduals ~ 1
## DW = 2.0251, p-value = 0.8587
## alternative hypothesis: true autocorrelation is not 0Teste de autocorrelação filogenética
Caso você tenha dados filogeneticamente estruturado, você pode prover uma matriz de distâncias filogenéticas para testar se há autocorrelação filogenética nos resíduos. Veja exemplos no help da função. Abaixo, apenas mostro um exemplo, mas nao funciona porque não tempos uma matriz filogenética
testPhylogeneticAutocorrelation(res, phylo = phylo) # nao funciona aqui, pois não temos uma matriz filogenética.Algumas outras funções
Fazer o histograma dos resíduos hist(); ver os resíduos residuals(); e plotar os resíduos contra uma variável preditora plotResiduals()*.
*Essa última função plotResiduals() é a mesma que apresentamos acima, mas agora motramos a opção de plotar os resíduos contra uma variável preditora. O que pode ser muit útil para verificar heterocedasticidade, por exemplo.
residuals(res)
(res)plotResiduals(res, form = testData$Environment1)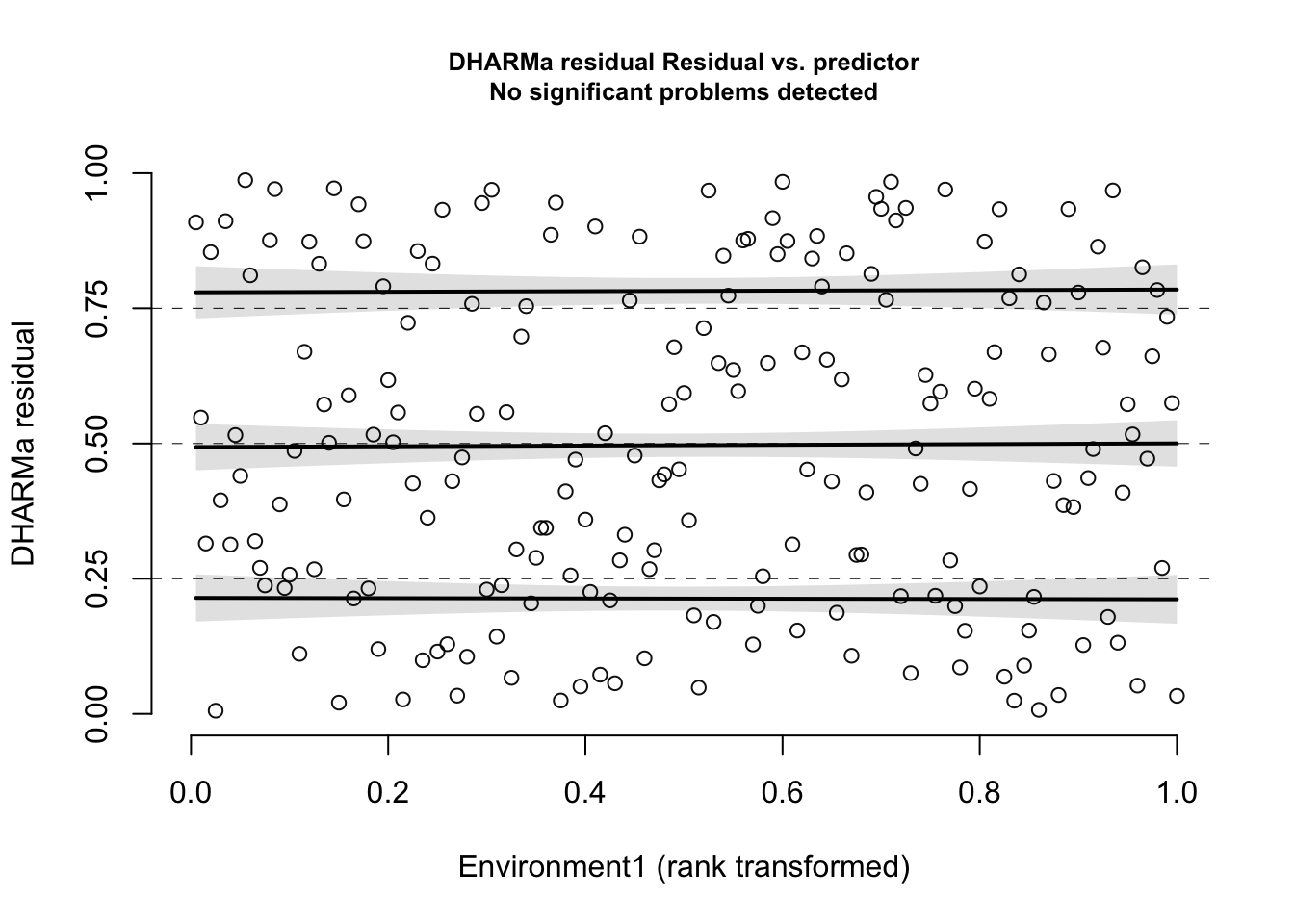
Alguns exemplos e possíveis problemas
Remover o efeito aleatório vai criar sobredispersão
Lembre-se que o nosso conjunto de dados tem uma estrutura agrupada (variável grupo). Se ignormarmos essa estrutura ajustando um GLM, podemos ver as consequências de um modelo incorretamente especificado através dos resíduos:
fittedModel2 <- glm(observedResponse ~ Environment1 ,
family = "poisson", data = testData)
res2 <- simulateResiduals(fittedModel = fittedModel2)
plot(res2)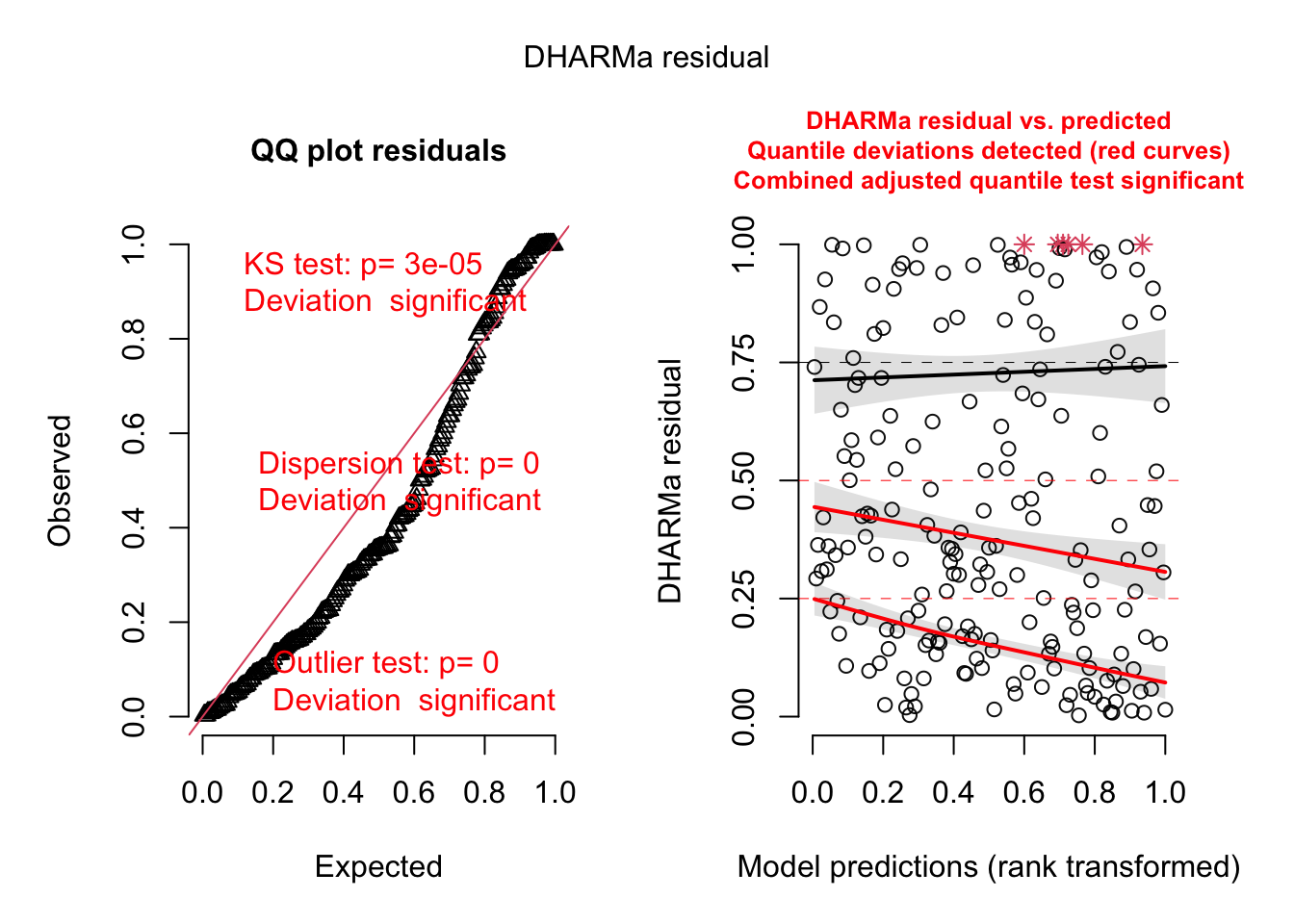
Veja como os resíduos agora não estão mais uniformemente distribuídos e os testes principais estão todos significativos. A forma meio S dos pontos observados no qqplot também indicam possível sobredispersão nos dados. Vamos ver o valor da dispersão:
testDispersion(res2)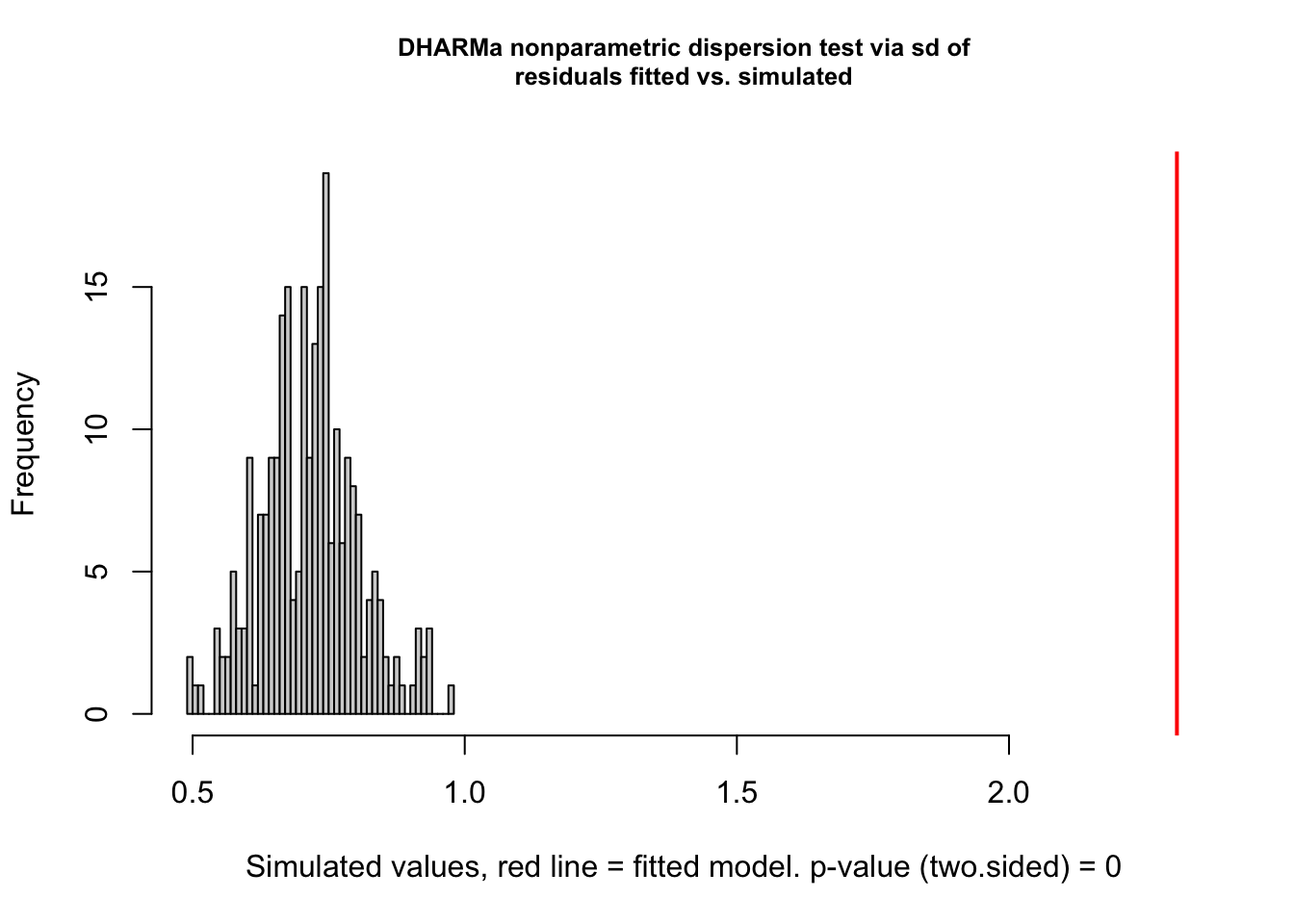
##
## DHARMa nonparametric dispersion test via sd of residuals fitted vs.
## simulated
##
## data: simulationOutput
## dispersion = 3.2236, p-value < 2.2e-16
## alternative hypothesis: two.sidedUm coeficiente de dispersão de 3 indica que a variância dos resíduos é 3 vezes maior do que a variância esperada pela distribuição Poisson. Isso é um sinal claro de sobredispersão. Veja o gráfico o quão longe está o valor de sobredispersão dos dados observados contra o histograma dos simulados.
OBS: Geralmente, em modelos Poisson, qualquer especificação equivocada do modelo vai indicar sobredispersão. Mas cuidado! Para resolver isso, não basta mudar para outra distribuição, por exemplo Binomial Negativa. Muitas vezes é mais adequando investigar melhor as possíveis causas, por exemplo preditores faltantes (incluindo ausência de efeito quadrático ou outra relação não-linear do preditor com a variável resposta), estrutura de agrupamento não considerada (exemplo acima), dados com inflação de zeros, etc.
Variável preditora faltante
Às vezes, a falta de um preditor importante pode não parecer problemático no diagnóstico geral. Aqui vamos ajustar um modelo sem a variável ambiental:
fittedModel3 <- glmer(observedResponse ~ 1 + (1|group),
family = "poisson", data = testData)
res3 <- simulateResiduals(fittedModel = fittedModel3)
plot(res3)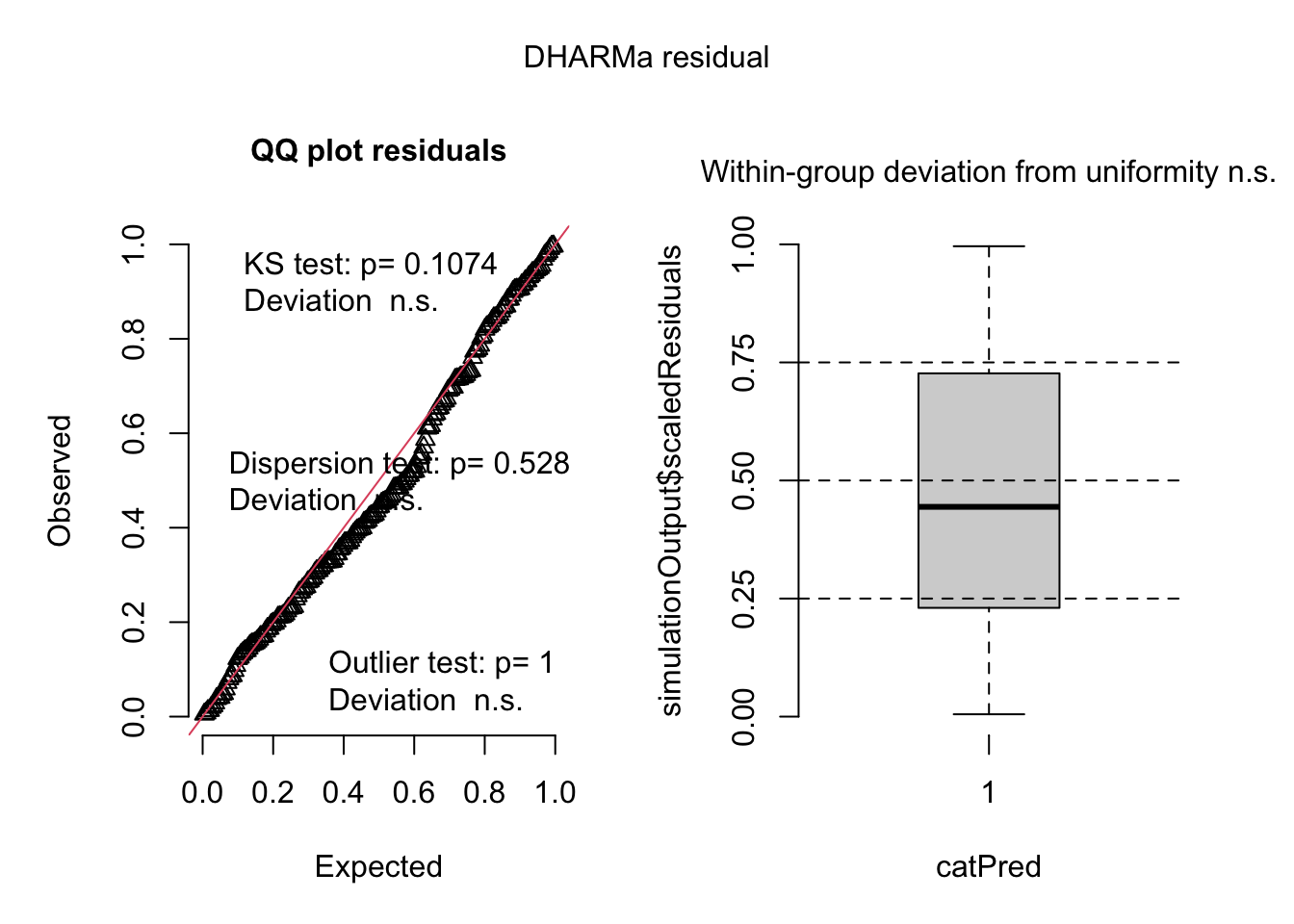
Repare que o gráfico Resíduos ~ Predito (direita) agora é um boxplot porque não há preditores no modelo, apenas o intercepto.
Mas, se a gente faz o gráfico dos resíduos contra a variável preditora (que a gentes sabe que criou os dados), podemos detectar o problema:
plotResiduals(res3, form = testData$Environment1)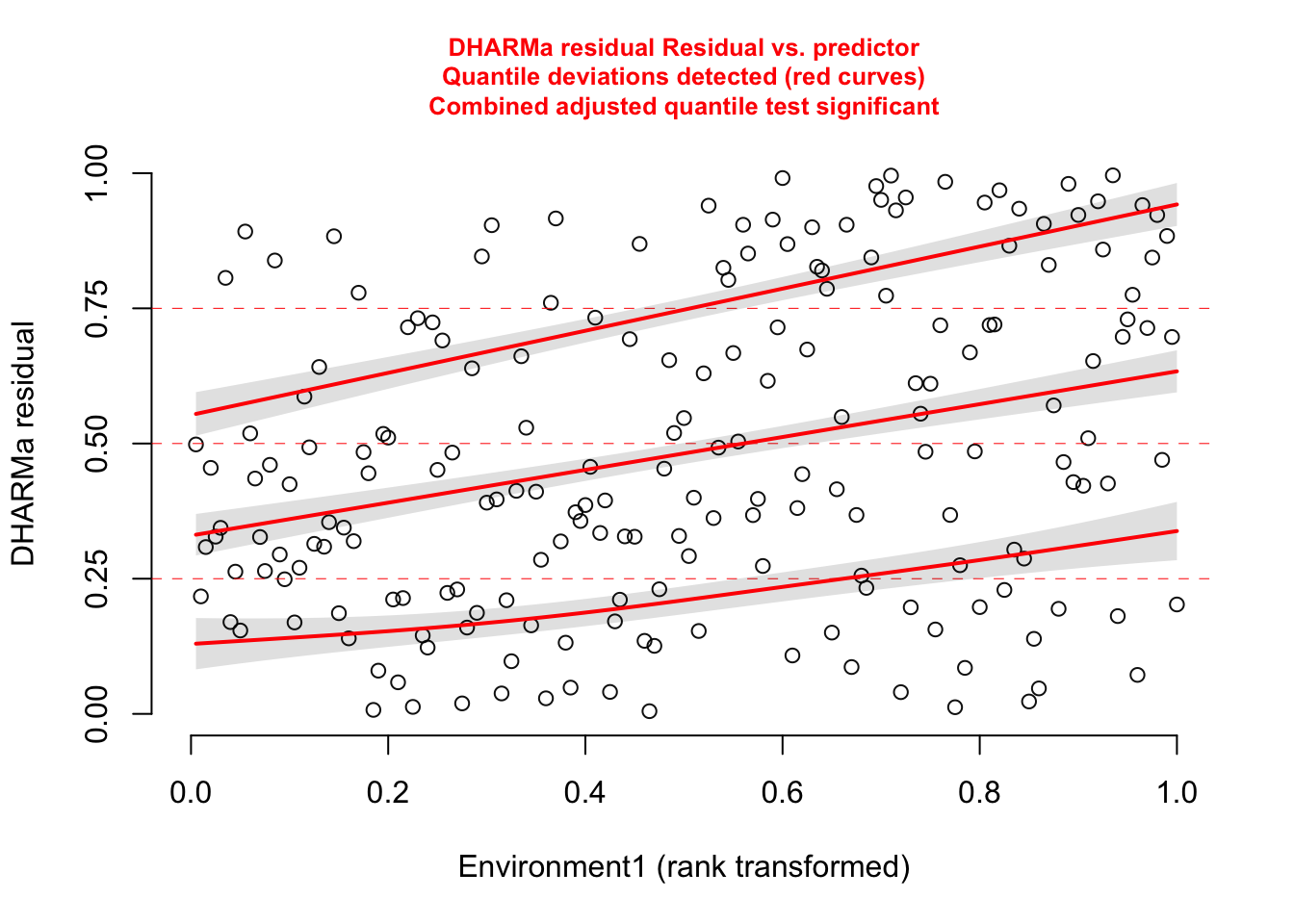
Agora a gente vê a falta do ajuste do modelo quanto à variável ambiental, já que os resíduos estão aumentando com o aumento da variável ambiental.
Conclusão: sempre verifique os resíduos contra todos os preditores! Não só os que já estão no modelo (ajuda a entender se uma relação linear é suficiente ou não e detectar heterocedasticidade), mas outros que vc tenha e que possam ter algum efeito na sua variável resposta.
Exemplo das corujas
Estes dados estão disponíveis no pacote glmmTMB (veja o help dos dados ?Olws ).
Vamos ajustar um modelo que segue a hipótese de que existe diferença no número de negociação dos filhotes entre os tratamentos de comida e o sexo do adulto alimentando (pai/mãe).
Olhando os dados:
library(glmmTMB)
ggplot(Owls, aes(x = FoodTreatment, y = SiblingNegotiation, fill=SexParent)) +
geom_boxplot() +
theme_bw()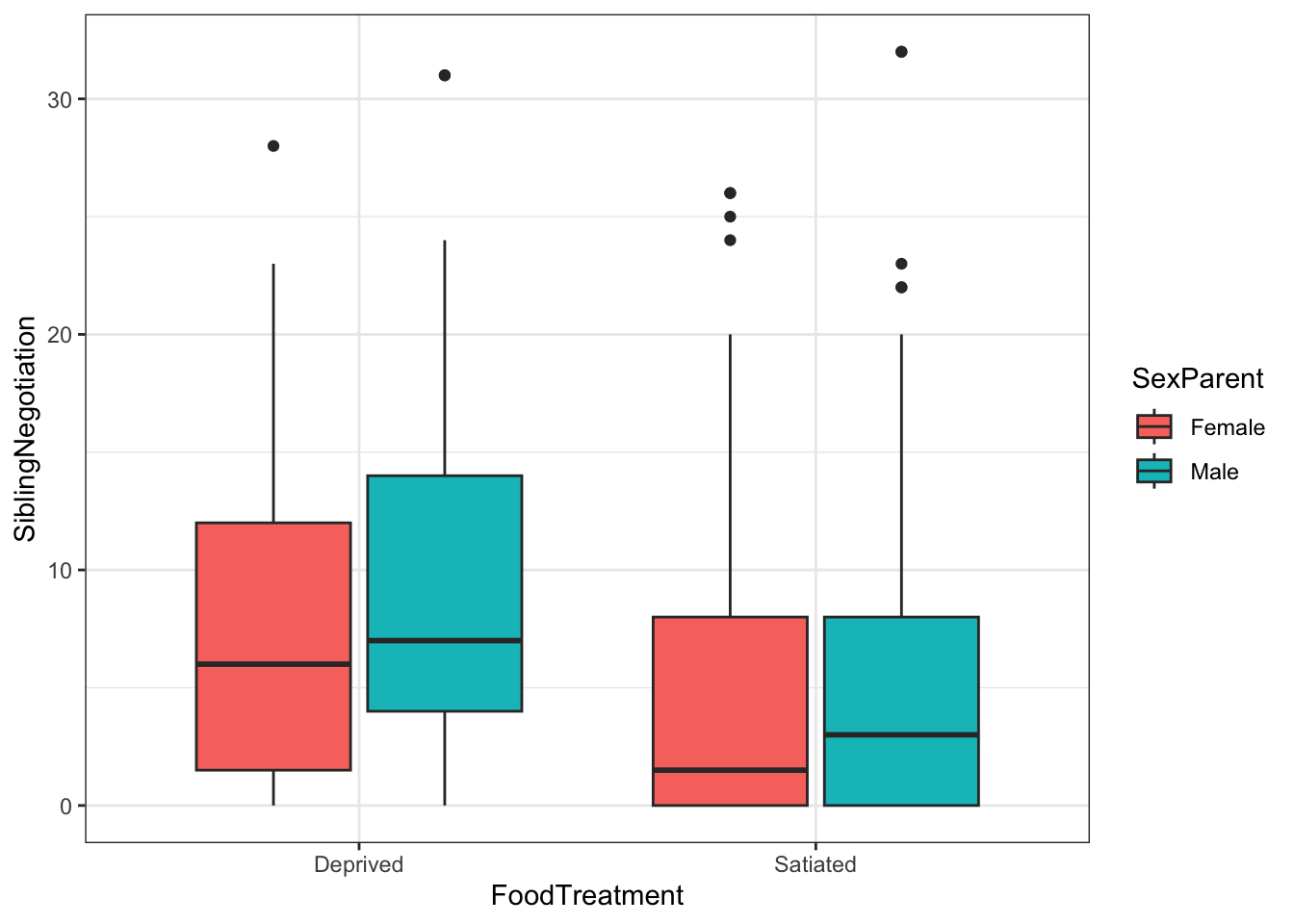
O modelo mais simples de todos é um glm poisson (dados de contagem) com interação entre os preditores e um offset para corrigir para o tamanho da ninhada.
m1 <- glm(SiblingNegotiation ~ FoodTreatment*SexParent + offset(log(BroodSize)), data=Owls , family = poisson)OBS: Para saber mais sobre o uso de “offsets” nos modelos, essa discussão pode ser útil e esse Preprint pode ajudar a entender melhor quando usar: Smith. 2024. Offset or not: guidance on accounting for sampling effort in generalized linear models. EcoEvoRxiv
Calculando os resíduos
res <- simulateResiduals(m1)
plot(res)## DHARMa:testOutliers with type = binomial may have inflated Type I error rates for integer-valued distributions. To get a more exact result, it is recommended to re-run testOutliers with type = 'bootstrap'. See ?testOutliers for details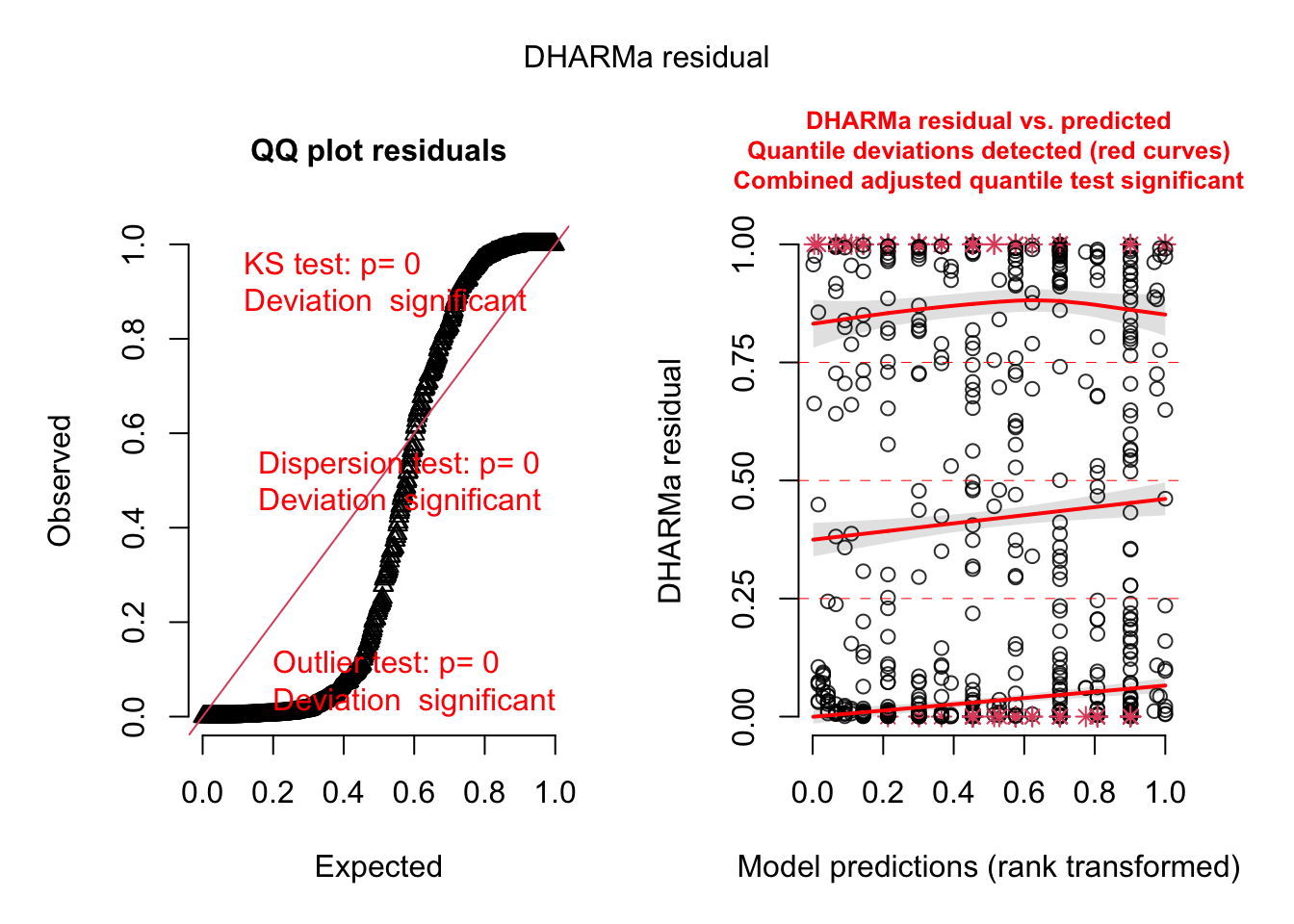
Claramente, há algo de errado neste modelo! Muito provavelmente, problema de sobredispersão, já que uma vez sobredisperso, vários outros testes (KS e outliers) vão dar significativo.
Olhando o teste de dispersão:
testDispersion(res)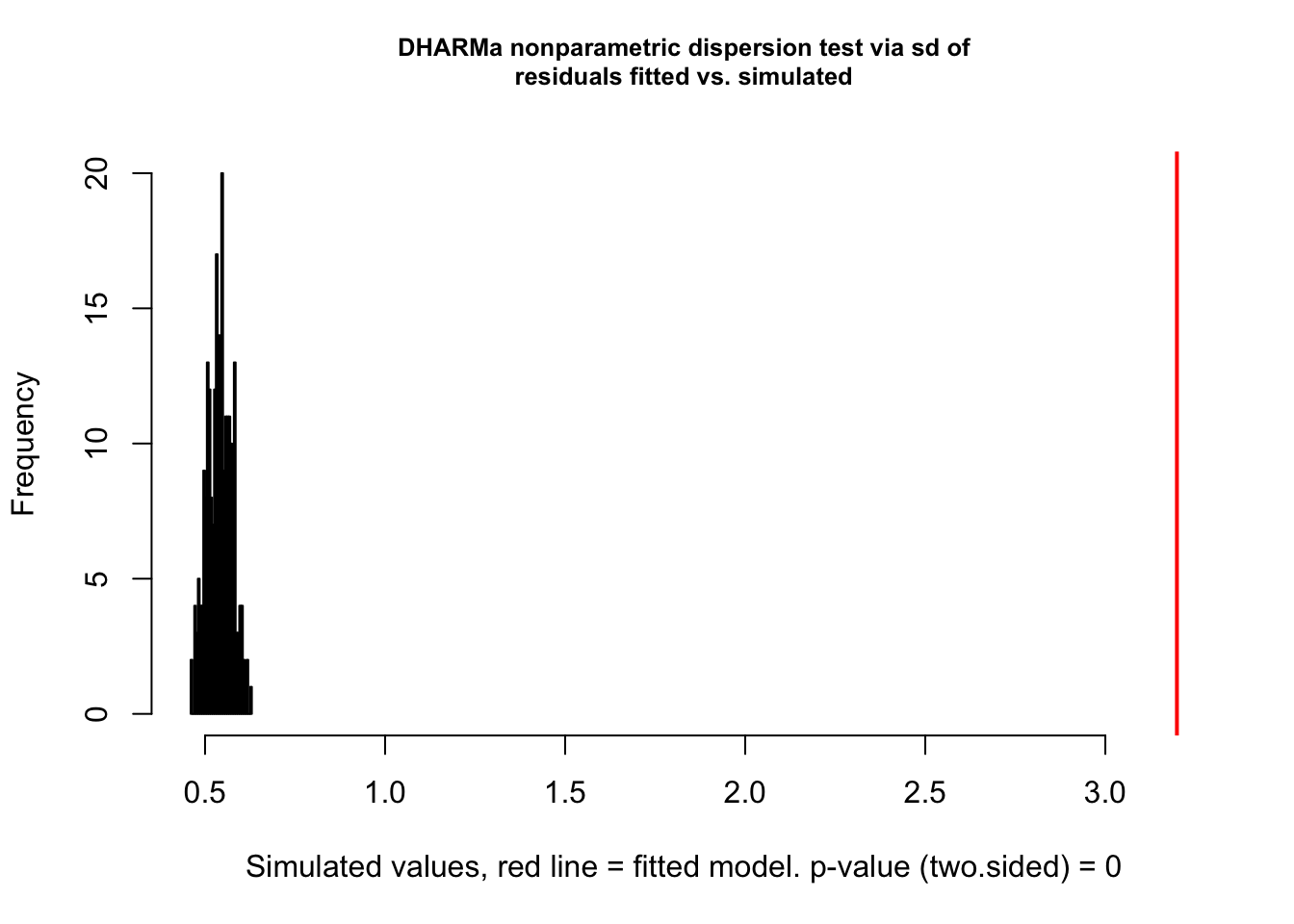
##
## DHARMa nonparametric dispersion test via sd of residuals fitted vs.
## simulated
##
## data: simulationOutput
## dispersion = 5.918, p-value < 2.2e-16
## alternative hypothesis: two.sidedPara resolver isso, vamos começar com um modelo misto (como fizemos antes), considerando que os dados são agrupados por ninho (se conhecessemos os dados já teríamos feito isso, mas por motivos didáticos, vamos adicioná-los só agora).
m2 <- glmer(SiblingNegotiation ~ FoodTreatment*SexParent + offset(log(BroodSize)) +
(1|Nest), data=Owls , family = poisson)
res2 <- simulateResiduals(m2)
plot(res2)## DHARMa:testOutliers with type = binomial may have inflated Type I error rates for integer-valued distributions. To get a more exact result, it is recommended to re-run testOutliers with type = 'bootstrap'. See ?testOutliers for details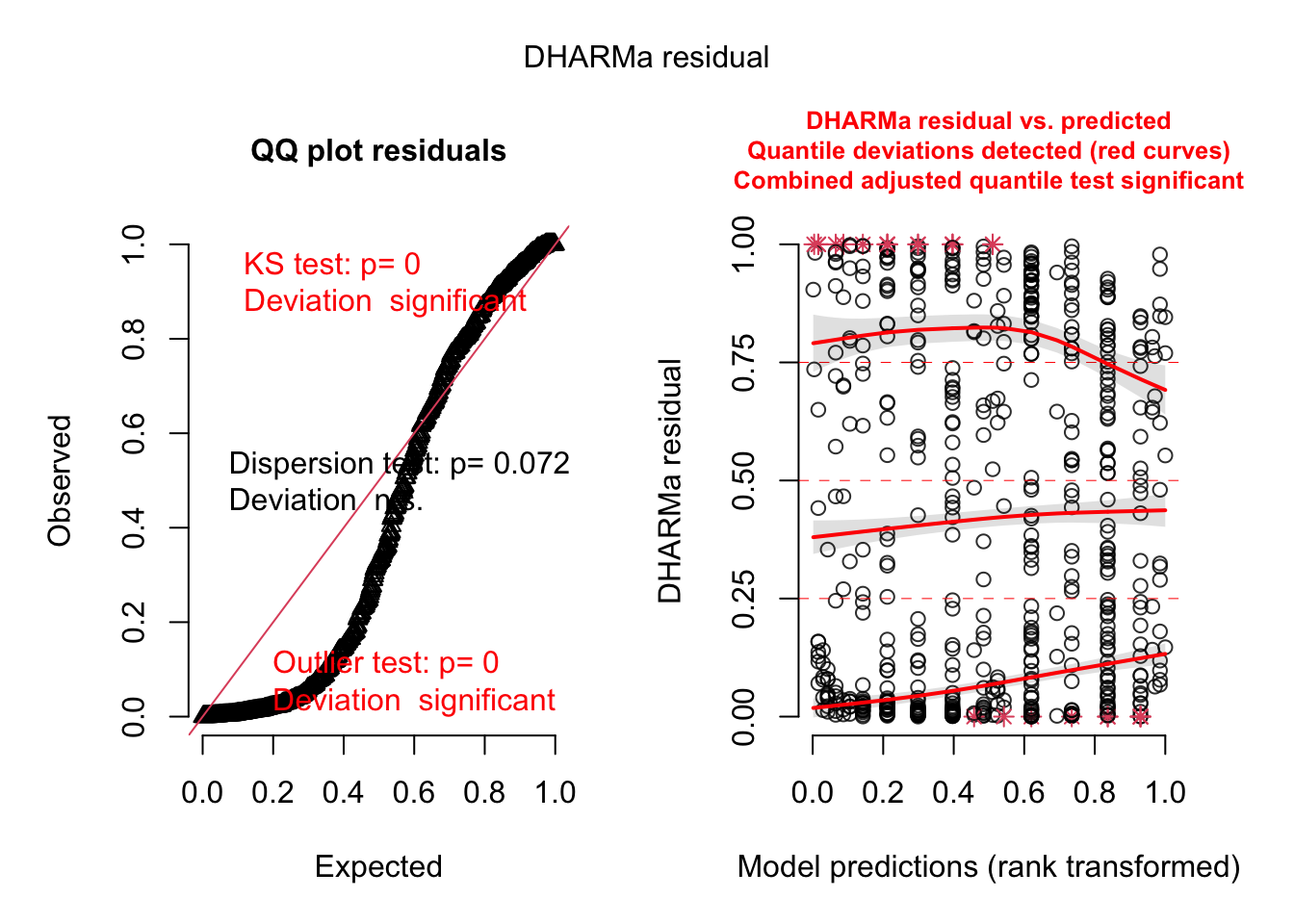
Os resíduos melhoraram, mas ainda parece que algo está errado. O teste de dispersão não deu significativo, mas vamos ver qual o valor do coeficiente de dispersão:
testDispersion(res2)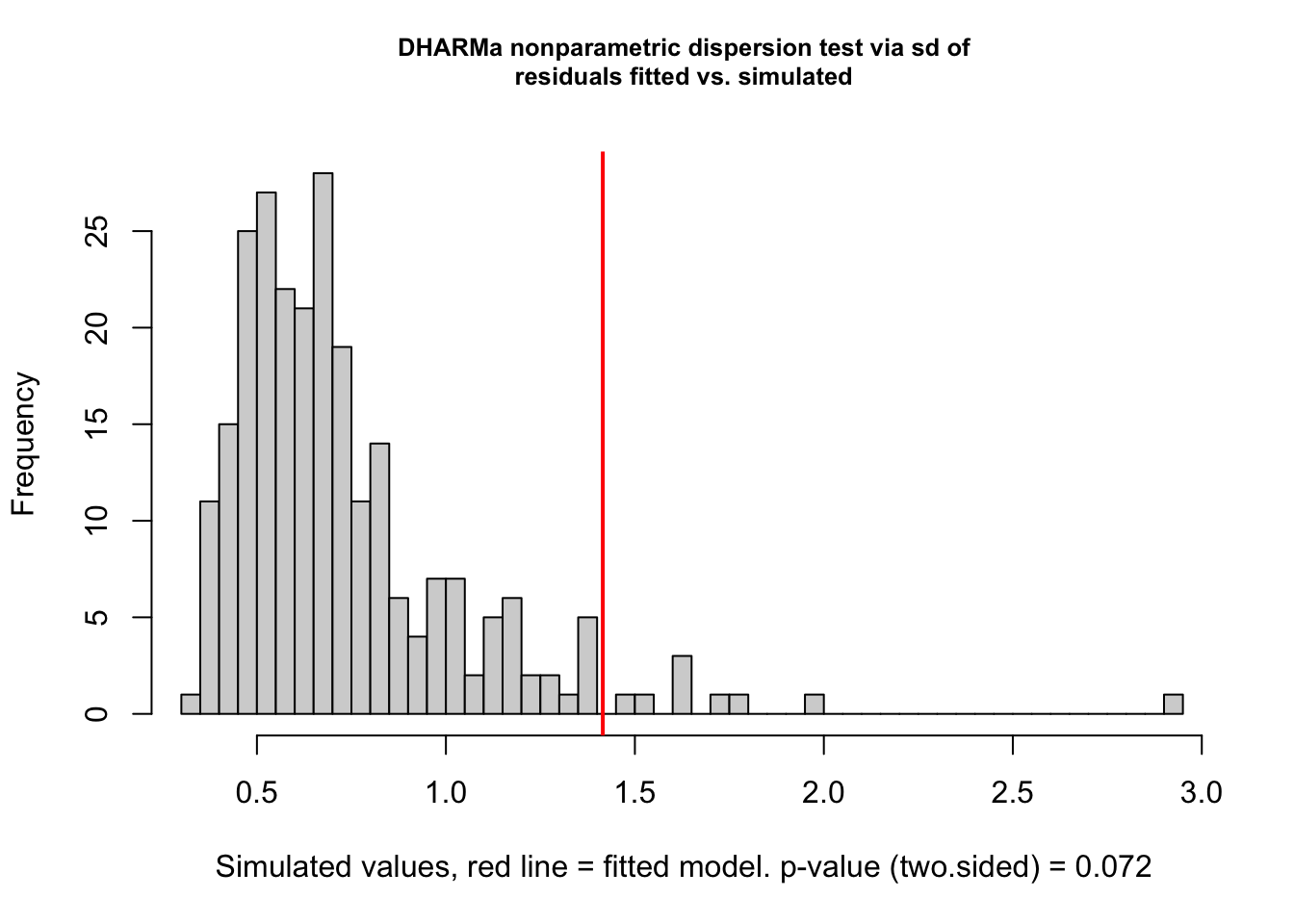
##
## DHARMa nonparametric dispersion test via sd of residuals fitted vs.
## simulated
##
## data: simulationOutput
## dispersion = 1.9418, p-value = 0.072
## alternative hypothesis: two.sidedBom, quase o dobro de dispersão (1,94) do que a esperada para a distrbuição Poisson (1,00). Vamos tentar, então, um modelo com a distribuição Binomial Negativa (geralmente uma das primeiras opções que as pesssoas pensam quando modelos Poisson não se comportam bem).
m3 <- glmmTMB(SiblingNegotiation ~ FoodTreatment*SexParent + offset(log(BroodSize)) +
(1|Nest), data=Owls , family = nbinom1)
res3 <- simulateResiduals(m3)
plot(res3)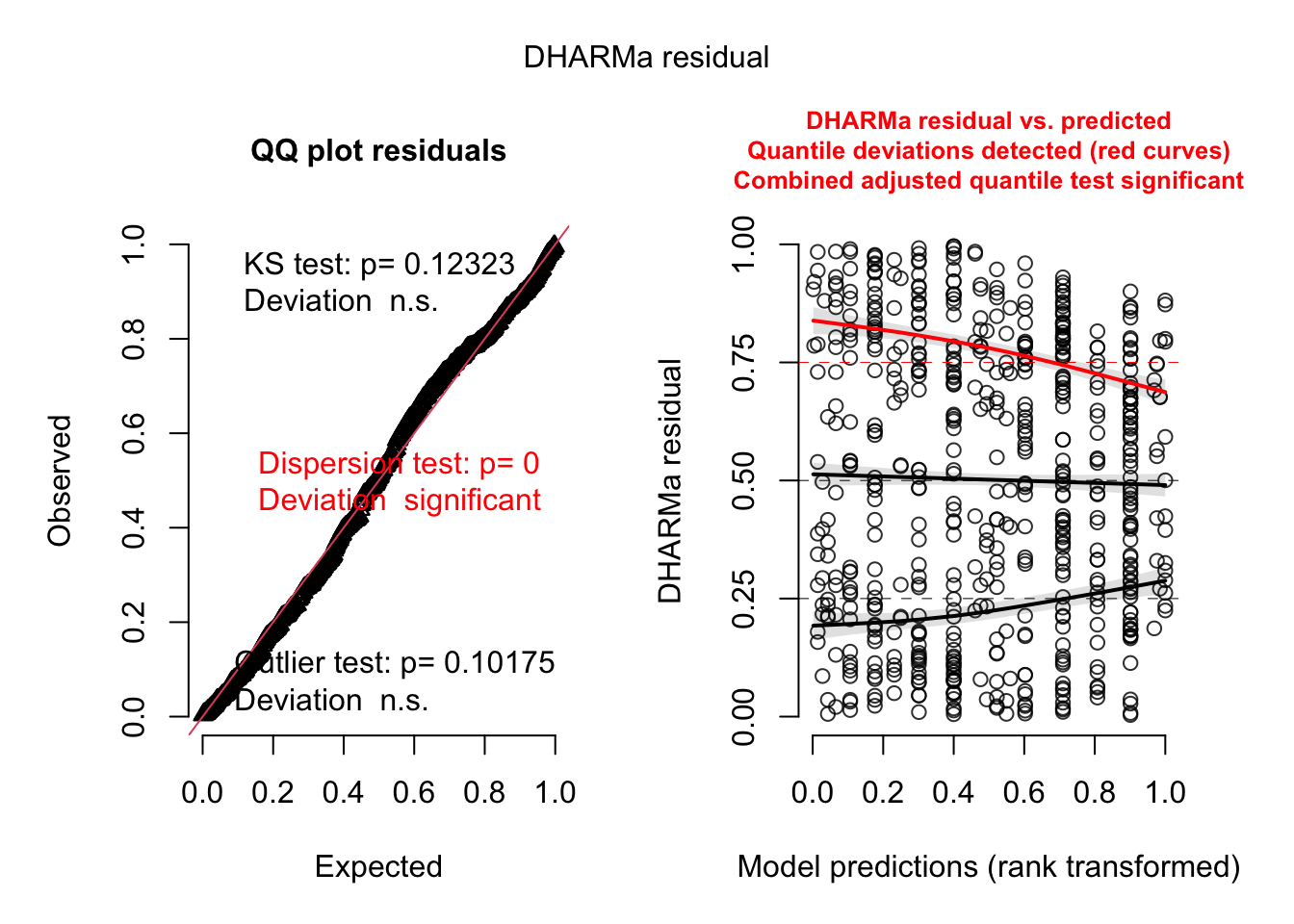
Ainda tem algo de errado aqui! Temos agora um problema de subdispersão, menos variância do que o esperado. Mas a Binomial Negativa tem um termo de dispersão que poderia ser flexível o suficiente para corrigir isso. Por quê então?
testDispersion(res3)
##
## DHARMa nonparametric dispersion test via sd of residuals fitted vs.
## simulated
##
## data: simulationOutput
## dispersion = 0.63438, p-value < 2.2e-16
## alternative hypothesis: two.sidedBem, o boxplot de exame dos dados acima não mostrou muito bem, mas o dotplot abaixo indica que existem um bocado e zeros nos dados.
ggplot(Owls, aes(x = FoodTreatment, y = SiblingNegotiation, fill=SexParent)) +
geom_dotplot(binaxis = "y", stackdir = "center", dotsize=0.4, alpha=0.4,
position = "dodge") +
theme_bw()## Bin width defaults to 1/30 of the range of the data. Pick better value with
## `binwidth`.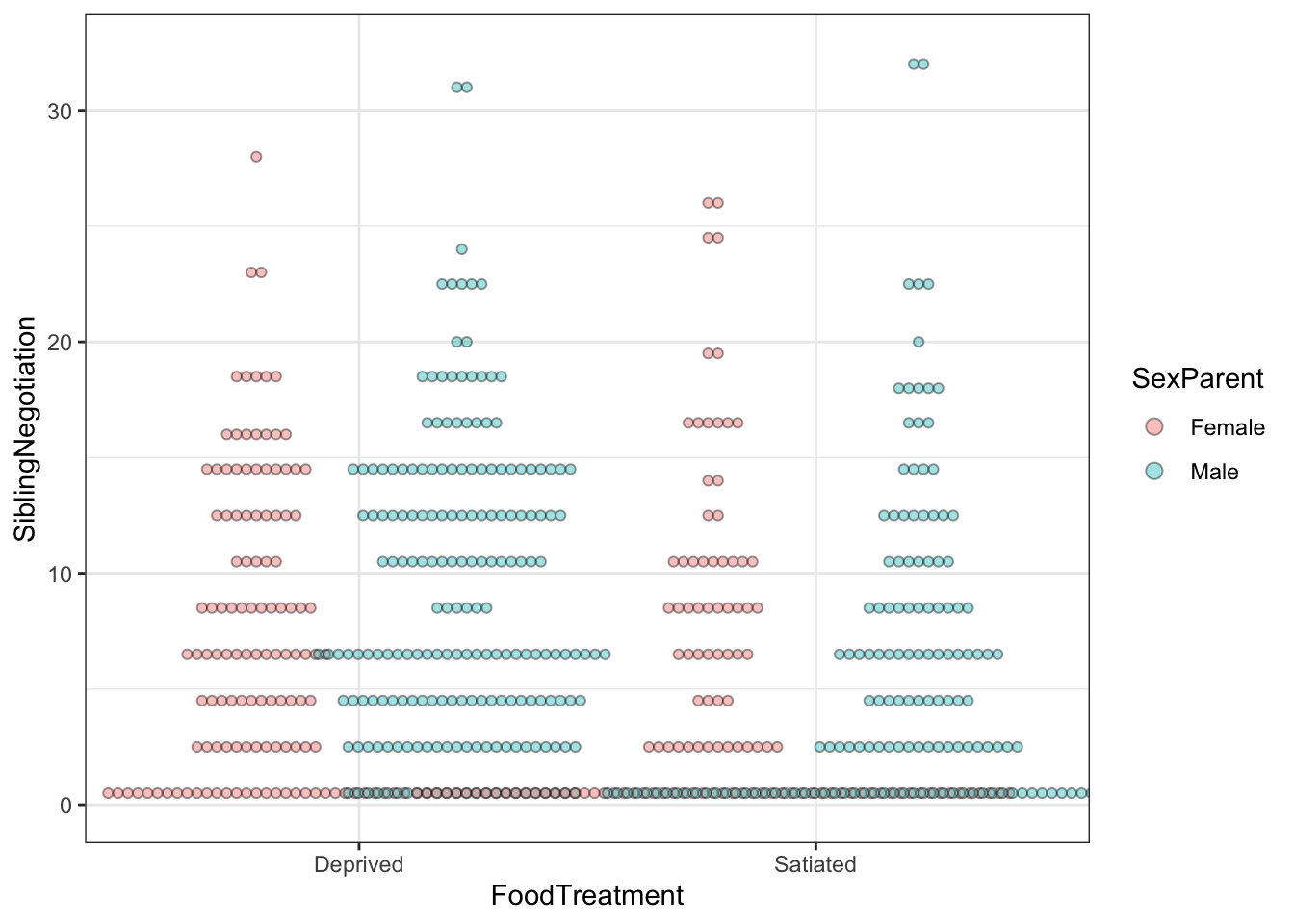
De fato, olhando para o banco de dados vemos que 1/4 (~26%) das observações são zeros:
sum(Owls$SiblingNegotiation == 0)/nrow(Owls)## [1] 0.2604341Vamos testar para zero-inflação:
testZeroInflation(res3)
##
## DHARMa zero-inflation test via comparison to expected zeros with
## simulation under H0 = fitted model
##
## data: simulationOutput
## ratioObsSim = 1.2488, p-value = 0.064
## alternative hypothesis: two.sidedParece que temos um problema de zero-inflação, embora apontado como não significativo (mas não se prenda tanto ao valor de p).
Então parece que o padrão de subdispersão num modelo cuja distribuição corrige para a dispersão (Binomial Negativa) é devido à zero-inflação. Uma razão possível é que o modelo se ajusta à inflação de zeros aumentando o parâmetro de dispersão, mas agora temos menos observações maiores do que o esperado, resultando em subdispersão.
Ajustando finalmente um modelo com zero inflação:
m4 <- glmmTMB(SiblingNegotiation ~ FoodTreatment*SexParent + offset(log(BroodSize)) +
(1|Nest),
ziformula = ~ FoodTreatment *SexParent, data=Owls , family = nbinom1 )
res4 <- simulateResiduals(m4)
plot(res4)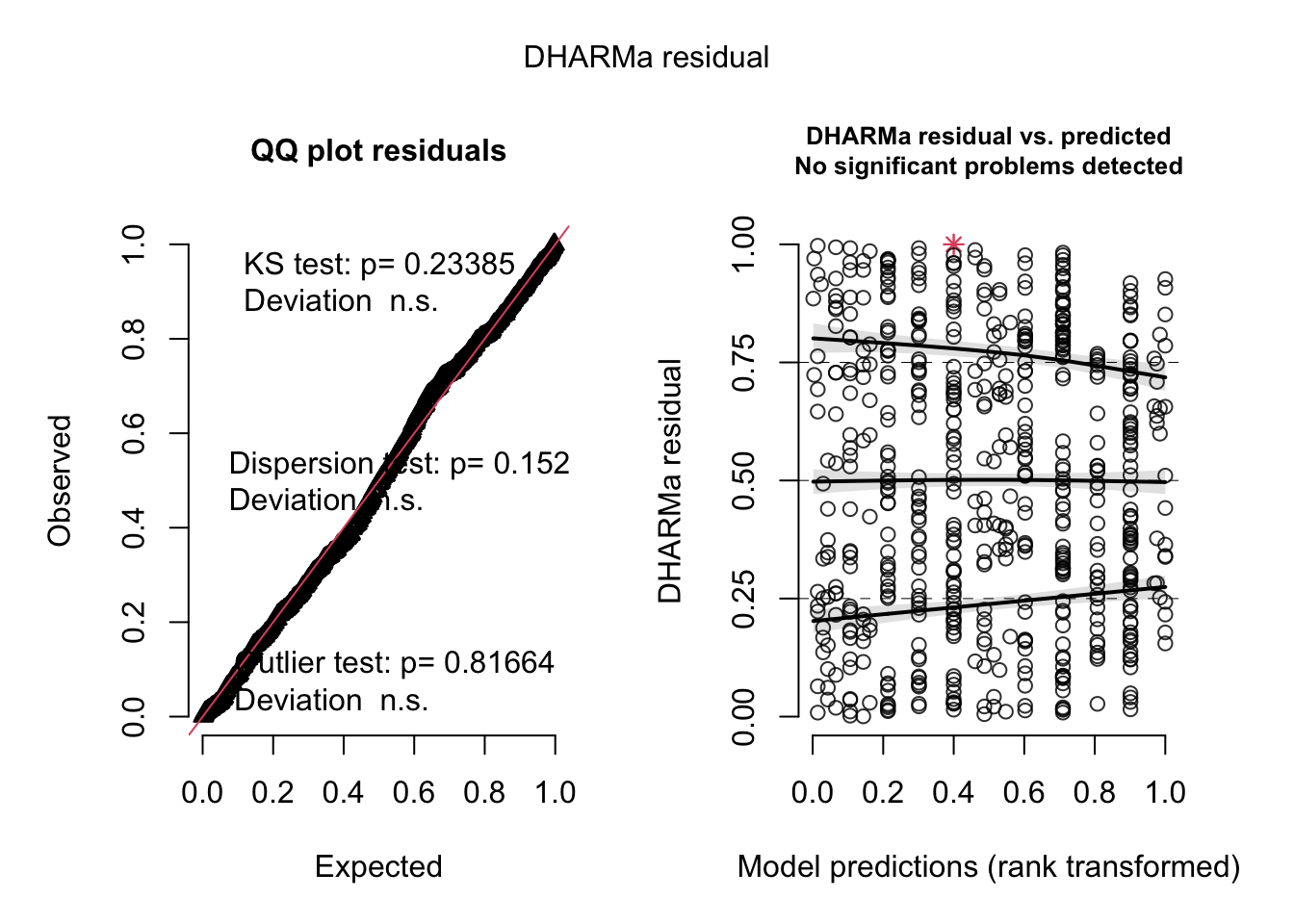
Apenas para ter certeza sobre usar ou não o modelo que controla zero-inflação podemos fazer uma simples comparação de modelos por AIC
bbmle::AICtab(m3,m4, base=T)## AIC dAIC df
## m4 3361.1 0.0 10
## m3 3400.8 39.7 6De fato, um modelo com zero-inflação se ajusta melhor aos dados.
Sugestões de estudos
Esse tutorial foi apenas um apanhado das funções e funcionalidades do DHARMa. Para um estudo mais aprofundado, sugiro:
- A Vinheta do pacote DHARMa tem outros exemplos e discute com muito mais profundidade as funções, os testes e diagnósticos de modelos.
- Exemplos reais também podem ser buscados nos issues do pacote no GitHub.
- Muitas dúvidas sobre o DHARMa e padrões nos resíduos já foram também respondidas no CrossValidated.
para alguns casos vale apena aumentar o número de simulações↩︎